量化理论源于论文: Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference
基本概念
INT8量化分为非对称量化和对称量化。对称量化是非对称量化的一个特例, 通常对称量化的性能会优于非对称量化, 而精度上非对称量化更优。
非对称量化
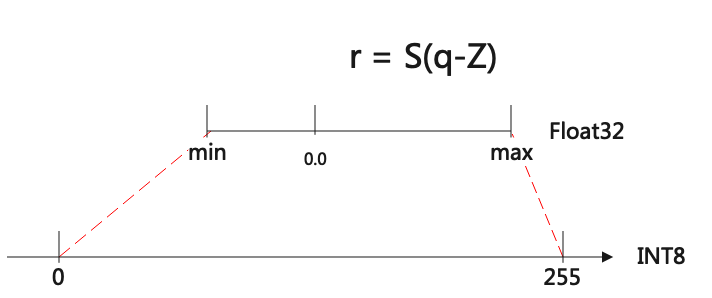
如上图(非对称量化)所示, 非对称量化其实就是把[min,max]范围内的数值定点到[-128, 127]或者[0, 255]区间。
从int8到float的量化公式表达如下:
\[\begin{split}r &= S(q-Z) \\
S &= \frac{max-min}{qmax-qmin} \\
Z &= Round(- \frac{min}{S} + qmin)\end{split}\]
其中r是真实的值, float类型; q是量化后的值, INT8或者UINT8类型;
S表示scale, 是float; Z是zeropoint, 是INT8类型;
当量化到INT8时, qmax=127,qmin=-128; UINT8时, qmax=255,qmin=0
反过来从float到int8的量化公式如下:
\[\begin{split}q = \frac{r}{S} + Z\end{split}\]
对称量化
对称量化是非对称量化Z=0时的特例, 公式表达如下:
\[\begin{split}i8\_value &= f32\_value \times \frac{128}{threshold} \\
f32\_value &= i8\_value \times \frac{threshold}{128}\end{split}\]
threshold是阈值, 可以理解为Tensor的范围是[-threshold, threshold]
这里 \(S = threshold / 128\), 通常是activation情况;
对于weight, 一般 \(S = threshold / 127\)
对于UINT8, Tensor范围是[0, threshold], 此时 \(S = threshold/ 255.0\)
Scale转换
论文中的公式表达:
\[\begin{split}M = 2^{-n}M_0, 其中M_0取值[0.5,1], n是一个非负数\end{split}\]
换个表述来说, 就是浮点数Scale, 可以转换成Multiplier和rshift, 如下表达:
\[\begin{split}Scale = \frac{Multiplier}{2^{rshift}}\end{split}\]
举例说明:
\[\begin{split}&y = x \times 0.1234 \\
&=> y = x \times 0.9872 \times 2^{-3} \\
&=> y = x \times (0.9872 \times 2^{31}) \times 2^{-34} \\
&=> y = x \times \frac{2119995857}{1 \ll 34} \\
&=> y = (x \times 2119995857) \gg 34\end{split}\]
Multiplier支持的位数越高, 就越接近Scale, 但是性能会越差。一般芯片会用32位或8位的Multiplier。
量化推导
我们可以用量化公式, 对不同的OP进行量化推导, 得到其对应的INT8计算方式。
对称和非对称都用在Activation上, 对于权重一般只用对称量化。
Convolution
卷积的表示式简略为: \(Y = X_{(n,ic,ih,iw)}\times W_{(oc,ic,kh,kw)} + B_{(1,oc,1,1)}\)
代入int8量化公式, 推导如下:
\[\begin{split}float:\quad & Y = X\times W + B \\
step 0\quad & => S_y(q_y-Z_y) = S_x(q_x-Z_x)\times S_wq_w + B \\
step 1\quad & => q_y - Z_y = S_1(q_x-Z_x)\times q_w + B_1 \\
step 2\quad & => q_y - Z_y = S_1 q_x\times q_w + B_2 \\
step 3\quad & => q_y = S_3 (q_x \times q_w + B_3) + Z_{y} \\
step 4\quad & => q_y = (q_x \times q_w + b_{i32}) * M_{i32} >> rshift_{i8} + Z_{y}\end{split}\]
非对称量化特别注意的是, Pad需要填入Zx
对称量化时, Pad填入0, 上述推导中Zx和Zy皆为0
在PerAxis(或称PerChannal)量化时, 会取Filter的每个OC做量化, 推导公式不变, 但是会有OC个Multiplier、rshift
Add
加法的表达式为: \(Y = A + B\)
代入int8量化公式, 推导如下:
\[\begin{split}float:\quad & Y = A + B \\
step 0\quad & => S_y (q_y-Z_y) = S_a(q_a-Z_a) + S_b(q_b - Z_b) \\
step 1(对称) \quad & => q_y = (q_a * M_a + q_b * M_b)_{i16} >> rshift_{i8} \\
step 1(非对称) \quad & => q_y = requant(dequant(q_a) + dequant(q_b))\end{split}\]
加法最终如何用TPU实现, 与TPU具体的指令有关。
这里对称提供的方式是用INT16做中间buffer;
在网络中,输入A、B已经是量化后的结果 \(q_a\)、 \(q_b\),因此非对称是先反量化成float, 做加法后再重量化成INT8
AvgPool
平均池化的表达式可以简写为: \(Y_i = \frac{\sum_{j=0}^{k}{(X_j)}}{k}, 其中k = kh \times kw\)
代入int8量化公式, 推导如下:
\[\begin{split}float:\quad & Y_i = \frac{\sum_{j=0}^{k}{(X_j)}}{k} \\
step0:\quad & => S_y(y_i - Z_y) = \frac{S_x\sum_{j=0}^{k}(x_j-Z_x)}{k}\\
step1:\quad & => y_i = \frac{S_x}{S_yk}\sum_{j=0}^{k}(x_j-Z_x) + Z_y \\
step2:\quad & => y_i = \frac{S_x}{S_yk}\sum_{j=0}^{k}(x_j) - (Z_y - \frac{S_x}{S_y}Z_x) \\
step3:\quad & => y_i = (Scale_{f32}\sum_{j=0}^{k}(x_j) - Offset_{f32})_{i8} \\
& 其中Scale_{f32} = \frac{S_x}{S_yk}, Offset_{f32} = Z_y - \frac{S_x}{S_y}Z_x\end{split}\]
LeakyReLU
LeakyReLU的表达式可以简写为: \(Y = \begin{cases} X, if X \geq 0\\ \alpha X, if X < 0 \end{cases}\)
代入int8量化公式, 推导如下:
\[\begin{split}float:\quad & Y = \begin{cases} X, if \ X \geq 0\\ \alpha X, if \ X < 0 \end{cases} \\
step0:\quad & => S_y (q_y - Z_y) = \begin{cases} S_x(q_x - Z_x), if \ q_x \geq 0\\ \alpha S_x (q_x - Z_x), if \ q_x < 0 \end{cases} \\
step1:\quad & => q_y = \begin{cases} \frac{S_x}{S_y}(q_x - Z_x) + Z_y, if \ q_x \geq 0\\ \alpha \frac{S_x}{S_y} (q_x - Z_x) + Z_y, if \ q_x < 0 \end{cases}\end{split}\]
对称量化时, \(S_y=\frac{threshold_y}{128}, S_x=\frac{threshold_x}{128}\), 非对称量化时, \(S_y = \frac{max_y - min_y}{255}, S_x = \frac{max_x - min_x}{255}\)。通过BackwardCalibration操作后, \(max_y = max_x, min_y = min_x, threshold_y = threshold_x\), 此时Sx/Sy = 1。
\[\begin{split}step2:\quad & => q_y = \begin{cases} (q_x - Z_x) + Z_y, if \ q_x \geq 0\\ \alpha (q_x - Z_x) + Z_y, if \ q_x < 0 \end{cases} \\
step3:\quad & => q_y = \begin{cases} q_x - Z_x + Z_y, if \ q_x \geq 0\\ M_{i8} >> rshift_{i8} (q_x - Z_x) + Z_y, if \ q_x < 0 \end{cases}\end{split}\]
当为对称量化时, Zx和Zy均为0。
Pad
Pad的表达式可以简写为: \(Y = \begin{cases} X, \ origin\ location \\ value, \ padded\ location \end{cases}\)
代入int8量化公式, 推导如下:
\[\begin{split}float:\quad & Y = \begin{cases} X, \ origin\ location \\ value, \ padded\ location \end{cases} \\
step0:\quad & => S_y (q_y - Z_y) = \begin{cases} S_x (q_x - Z_x), \ origin\ location \\ value, \ padded\ location \end{cases} \\
step1:\quad & => q_y = \begin{cases} \frac{S_x}{S_y} (q_x - Z_x) + Z_y, \ origin\ location \\ \frac{value}{S_y} + Z_y, \ padded\ location \end{cases}
\end{split}\]
通过ForwardCalibration操作后, \(max_y = max_x, min_y = min_x, threshold_y = threshold_x\), 此时Sx/Sy = 1。
\[\begin{split}step2:\quad & => q_y = \begin{cases} (q_x - Z_x) + Z_y, \ origin\ location \\ \frac{value}{S_y} + Z_y, \ padded\ location \end{cases}
\end{split}\]
对称量化时, Zx和Zy均为0, pad填入 round(value/Sy), 非对称量化时, pad填入round(value/Sy + Zy)。
PReLU
PReLU的表达式可以简写为: \(Y_i = \begin{cases} X_i, if \ X_i \geq 0\\ \alpha_i X_i, if \ X_i < 0 \end{cases}\)
代入int8量化公式, 推导如下:
\[\begin{split}float:\quad & Y_i = \begin{cases} X_i, if \ X_i \geq 0\\ \alpha_i X_i, if \ X_i < 0 \end{cases} \\
step0:\quad & => S_y (y_i - Z_y) = \begin{cases} S_x (x_i - Z_x), if \ x_i \geq 0\\ S_{\alpha}q_{\alpha_i}S_x (x_i - Z_x), if \ x_i < 0 \end{cases} \\
step1:\quad & => y_i = \begin{cases} \frac{S_x}{S_y} (x_i - Z_x) + Z_y, if \ x_i \geq 0\\ S_{\alpha}q_{\alpha_i}\frac{S_x}{S_y} (x_i - Z_x) + Z_y, if \ x_i < 0 \end{cases} \\
\end{split}\]
通过BackwardCalibration操作后, \(max_y = max_x, min_y = min_x, threshold_y = threshold_x\), 此时Sx/Sy = 1。
\[\begin{split}step2:\quad & => y_i = \begin{cases} (x_i - Z_x) + Z_y, if \ x_i \geq 0\\ S_{\alpha}q_{\alpha_i}(x_i - Z_x) + Z_y, if \ x_i < 0 \end{cases} \\
step3:\quad & => y_i = \begin{cases} (x_i - Z_x) + Z_y, if \ x_i \geq 0\\ q_{\alpha_i} * M_{i8} (x_i - Z_x) >> rshift_{i8} + Z_y, if \ x_i < 0 \end{cases} \\
\end{split}\]
一共有oc个Multiplier和1个rshift。当为对称量化时, Zx和Zy均为0。