在对激活进行伪量化前先将激活截断在(0,1)之间, 这样的做法是基于一些经典的网络结构中,比如AlexNet与RestNet中,大部分的激活都会落在这个范围里的。
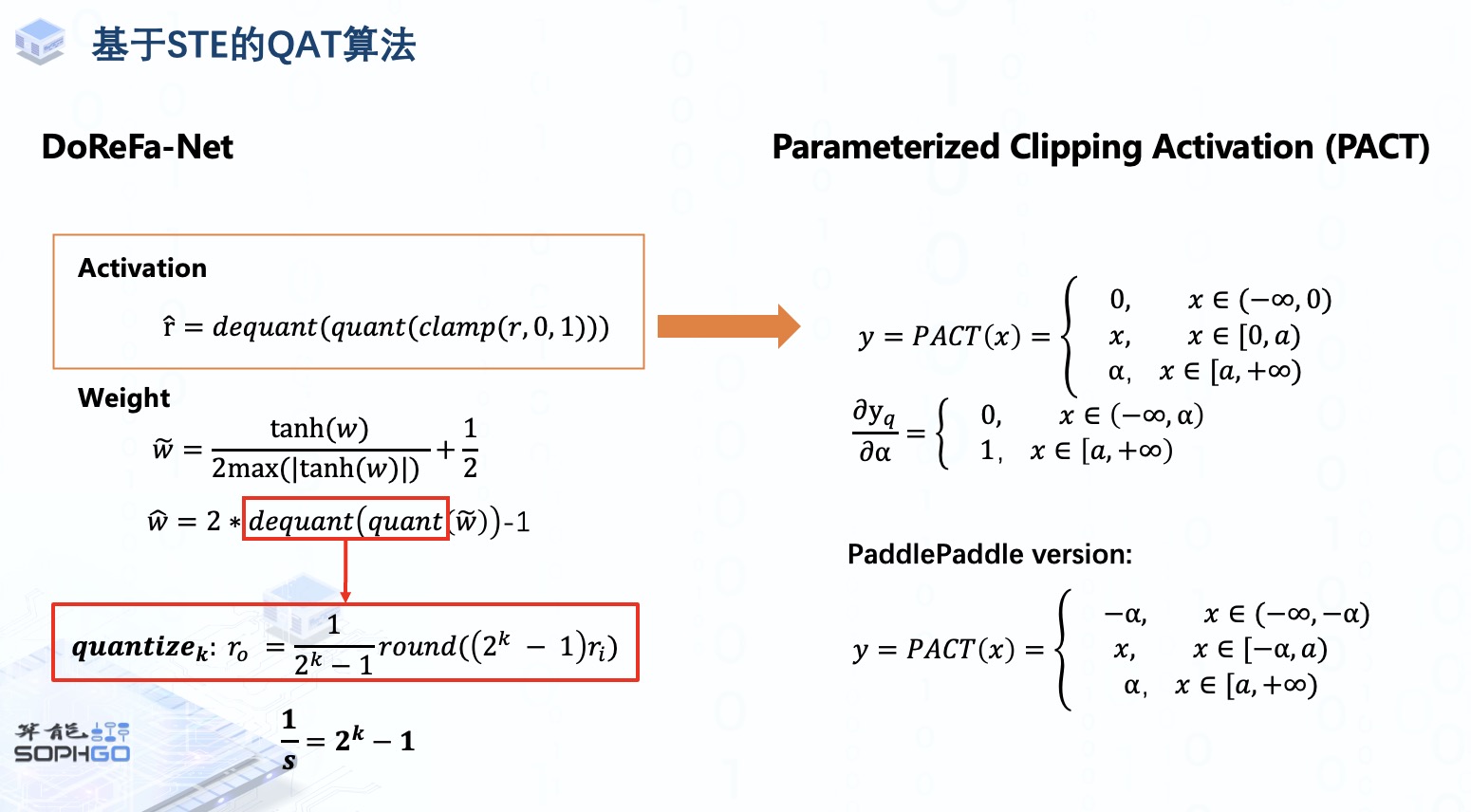
对于weight,则是先通过这样的一个非线性函数对weight进行映射,tanh(w)将weight的值域缩放到-1到+1之间,再除以2倍的tanh(w)绝对最大值加上1/2最终weight被映射到了0到1之间,再对其进行量化与反量化,再将输出结果通过乘2减1仿射变换到-1到1之间。
这里的quant与dequant操作在原论文中是被表示为一个quantize_k的操作,k指的是k位的量化,其实本质上就和我们之前提到的量化公式相似,就是把1/s替换成了2^k-1。
但DoReFa-Net的这个方式对于其它一些activation取值分布较广的网络就显得有点过于死板了,所以就有另一个改进版本的算法Parameterized Clipping Activation,PACT针对activation的伪量化这一部分,将截断门限alpha设为可学习的参数,然后通过梯度下降来寻找更优的门限。
因为alpha被设为可学习参数,所以这一部分的导数就可以由小于alpha的部分为0,大于等于alpha的部分为1。
大家看到PACT的这个函数其实和ReLU很像,对大于零的部分做一个截断操作,其实PACT原本思想也是想要替代ReLU。但问题是并非所有的模型结构用的都是ReLU这个激活函数,所以为了让PACT的应用范围更广,PaddlePaddle也也对其做了一定的改进,对大于零和小于零的激活值都做了相同的限制,使它能够在某些情况下得到更好的量化范围,以降低量化损失。
除此之外,还有一个常被使用到的算法,Learned Step Size Quantization,与PACT相似的是它也是通过训练来确定量化参数,但不同的是PACT学习的是截断门限,而LSQ直接将Scale定为一个可学习的参数。

我们先来看它的计算公式,这里的r_hat指的就是经过量化与反量化后的数值,
这其实就是在对称量化公式的基础上加了个scale,完成了一个量化与反量化的过程
因为我们需要反向传播计算梯度,所以就要对这个公式进行求导 (加些对公式的解说)
对于这一块的导数,LSQ还是采用直通估计,由此我们就得到了一个最终的导数公式;
这里又可以看出,LSQ虽然也采用了直通估计,但它在截取范围内还是存在梯度计算的
而且,为了使得Scale的学习更为稳定,LSQ还为其梯度加上了一个缩放系数,这个系数主要由tensor中的元素数量决定
另外,既然是可学习参数,那么就需要为其设置一个初始值,PACT中的alpha通常会被手动设置为常数值6,而LSQ原文中scale的初始值则由tensor的L1正则确定,不过在实践过程中,其实更多的是通过统计激活分布,用EMA-minmax, KLD,MSE等PTQ的方式来计算初始的scale值